

Infinite PathsIrrationals and Infinite Paths: If {$a$}, {$b$}, and {$c$} are linearly independent as vectors over the field of rational numbers and {$a,b<c<a+b$}, then the path on the {$a\times b\times c$} box is infinite. We proved (the fine structure of the box triangle) that the middle of the box triangle looks like this: 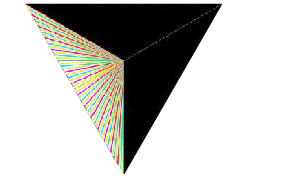 There are just three colors in the non-black part (so just three possible destinations). And there are also white lines. In all the boxes along a white line the path is infinite. Here is the exact story. When the Lines are White: For any {$0<r<\frac12$}, the path on the {$r\times \left(\frac12-r\right)\times \frac12$} box reaches a corner iff {$r$} is rational. 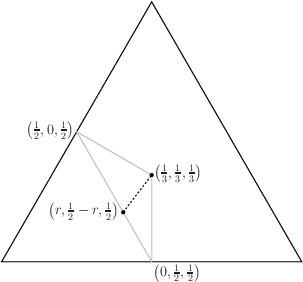 A box with dimensions {$a$}, {$b$}, {$c$} where {$a\le b<c\le a+b$} corresponds to a point {$(6r-2)t+2$}, {$(1-6r)t+2$}, {$t+2$}, where {$0\le r\le \frac12$} and {$0\le t\le 1$}. In that case, {$r$} is rational iff {$\frac{c-a}{c-b}$} is rational. This gives us Corollary: If {$a\times b\times c$} is a triangular box, then the path is infinite iff {$\frac{c-a}{c-b}$} is rational. This fits well with Destinations of Paths on Triangular Boxes. |