

When the Lines are White:For any {$0<r<\frac12$}, the path on the {$r\times \left(\frac12-r\right)\times \frac12)$} box reaches a corner iff {$r$} is rational. 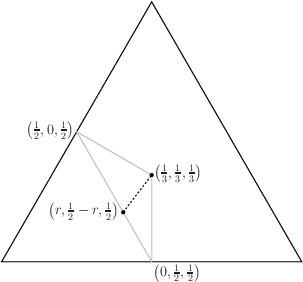 Proof: Using the overhead view, 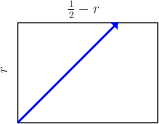 we see that since the height of the box is the sum of the other two dimensions, climbing up the walls takes you to the point exactly opposite to where you started. 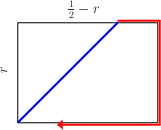 Now compare this path with the path of a ball bouncing inside the rectangle of the base. 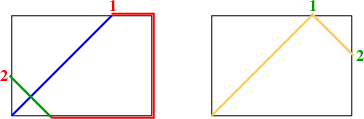 As the paths continue,  they are either at opposite points or at the same point. Thus one path ends at a corner iff the other does. Such billiard paths on a rectangle end iff the ratio of the dimensions is rational (Infinite Billiard Paths). In this case, the ratio is {$$\frac1{2r}-1,$$} which is rational iff {$r$} is. |