

Irrationals and Infinite Paths:If {$a$}, {$b$}, and {$c$} are linearly independent as vectors over the field of rational numbers and {$a,b<c<a+b$}, then the path on the {$a\times b\times c$} box is infinite. Proof: Recall the picture we get from rolling the box on the plane. 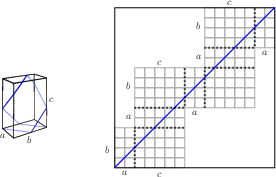 The diagram is contained in a square. Each side of the square is a linear combination of {$a$}, {$b$}, and {$c$}. In the case above, the square is {$3a+2c$} wide and {$3b+2a$} high. The sums of the coefficients in the linear expressions note the number of times each dimension of the box is traversed. For example, the sum of the coefficients of {$a$} is 5 and indeed the short side {$a$} is crossed five times in the path. The sums of the coefficients of {$a$} and {$b$} are odd; the sum of the coefficients of {$c$} is even and so the destination of the path is {$110$}. Call a triple {$(a,b,c)$} "balanced" if in the rolling picture, the coefficients of {$a$}, {$b$}, and {$c$} in the expressions for the lengths of the sides of the unfolding are identical. Now suppose for linearly independent {$a$}, {$b$}, {$c$}, that the path is finite. Consider the unfolding. The sides of the square containing the unfolding will each be linear combinations of {$a$}, {$b$}, and {$c$}; as sides of a square, they will be equal. Since {$a$}, {$b$}, {$c$} are linearly independent, we must have that the coefficients for the two sides are identical, so {$(a,b,c)$} is balanced. That means that the sums of the two coefficients for each of {$a$}, {$b$} and {$c$} are even. Hence the destination of the path is {$000$}. The Open Claim: The set of points in the box triangle whose barycentric coordinates are balanced is open. Using the claim, we can choose rationals {$r'$}, {$s'$}, {$t'$} approximating {$r$}, {$s$} and {$t$} which have an equivalent unfolding, that is, the path on the {$r'\times s'\times t'$} box also has destination corner {$000$}. But we will still have {$r',s'<t'<r'+s'$} and by the corollary to the Center Third theorem, the destination can only be one of {$101$}, {$110$}, or {$011$}. This is a contradiction and the Proposition is proved. |