

Destinations of Paths on Triangular Boxes:If {$a,b\le c<a+b$}, then
Proof: Note first that in view of Just Right, any path starting on one of the four walls of the box (instead of the bottom or top) must end at the corner where it began, travelling on the adjacent wall.  Every path that ends on a wall is part of a loop that begins on a wall, so no path that ends on a wall can begin on the bottom or top. Thus, a path starting on the bottom face must end running along the bottom face or end on the top face. To see what is going on when we start along the bottom, we use the overhead view. We draw a checkerboard pattern on the bottom and top faces of the box to see which corners are possible destinations and which are not. We use the same pattern for top and bottom with the lower-left corner gray. As an example, consider a box with dimensions {$(7,5,10)$}. Seen from above, the path starts like this on the floor, 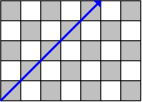 then continues like this as it climbs up the walls of the box. 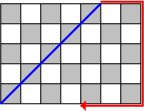 The path continues on the top of the box, 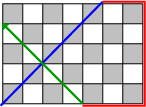 and then down the walls of the box. 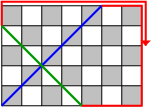 Notice that on the bottom the path moves SW-NE ↗ or NE-SW ↙ and on the top the path moves SE-NW ↖ or NW-SE ↘ . The Two Corners Claim: Seen from the top, as the path moves on the walls it always passes exactly two corners. The Direction Claim: Seen from the top, the path always moves SW-NE or NE-SW on the bottom and SE-NW or NW-SE on the top. The Gray-White Claim: The path on the bottom always moves on gray squares. The path on the top always moves on gray squares if $c$ is odd; it always moves on white squares if $c$ is even. The proof of the Theorem now proceeds by cases. |