

GCD{$\ \cdot\ $}LCM = PROD for Generic Boxes:If {$T\in\mathcal {B}^+$} is generic, then {$$\text{GCD}_{_T}\cdot\text{LCM}_{_T}=\text{PROD}_{_T}.$$} Proof: Since {$a_{_T}+b_{_T}>c_{_T}$} ({$T$} is not a rim), {$\Delta(\langle a_{_T},b_{_T},c_{_T}\rangle)=\langle a_{_T},b_{_T},c_{_T}-a_{_T}-b_{_T}\rangle$} and {$x_{_T}=a_{_T}+b_{_T}-c_{_T}$}. The most difficult step in this proof is the first, verifying the proposition when the box is triangular, {$T=\langle a_{_T},b_{_T},c_{_T}\rangle$}. The Triangular Generic Claim: If {$T\in\mathcal {B}^+$} is triangular and generic, then {$$\text{GCD}_{_T}\cdot\text{LCM}_{_T}=\text{PROD}_{_T}.$$} To conclude the proof, we must show that if {$\text{GCD}_{_T}\cdot\text{LCM}_T=\prod_{_T}$} holds for a generic box {$T$}, then it holds for all three {$\Delta$} pre-images of {$T$}. We assume then, that {$\text{GCD}_{_T}\cdot\text{LCM}_T=\prod_{_T}$} holds for {$T=\langle r,s,t\rangle$}. As in the proof of Proposition 20, we will need to add the same set of equations to the induction hypothesis: {$$\text{GCD}_{_T}\left[\begin{array}{ccc}p^1_a&p^1_b&p^1_c\\ p^1_a+p^3_a&p^1_b+p^3_b&p^1_c+p^3_c\end{array} \right]=K(T_v).$$} We must then show
For 1. and 2., the proofs are identical to the corresponding proofs in the Theorem for Spokes. For 3., we need to find the path vectors for {$L_1=L_2$} and {$L_3$}. The path vector for {$L_1$} is simple. From Just Right, the path returns quickly to the start, 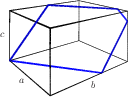 so the path vector is {$(2,2,2)$}. For {$P^3$}, we return to the connection with the {$(c_{_T}-b_{_T})\times(c_{_T}-a_{_T})$} rectangle. 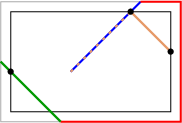 The number of times the geodesic climbs or traverses the walls is one less than the number of diagonal pieces of the billiard ball path. That's {$p^3_c=n-1=\frac {c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2$}. For {$p^3_a$}, note that on the rectangle, the {$a_{_T}-x_{_T}$} side is traversed {$\frac{b_{_T}-x_{_T}}d=\frac{c_{_T}-a_{_T}}d$} times. In addition, every time the walls are climbed the geodesic rounds exactly two corners. That means it finishes both a traverse of the {$a_{_T}-x_{_T}$} side and a traverse of the {$b_{_T}-x_{_T}$} side. Thus, {$$p^3_a=\frac {c_{_T}-a_{_T}}d+\frac {c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2 =2\frac {c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2.$$} Similarly, {$$p^3_b=\frac {c_{_T}-b_{_T}}d+\frac{c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2 =\frac{c_{_T}-a_{_T}}d+2\frac{c_{_T}-b_{_T}}d-2.$$} Now we compute: {$$\begin{array}{rcl}&&\text{GCD}_{_T}\cdot(p^1_a,p^1_a+p^3_a)\\ &=&(a_{_T}+b_{_T}-c_{_T},d)\cdot(2,2+2\frac {c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2)\\ &=&2a_{_T}+2b_{_T}-2c_{_T}+2d+2c_{_T}-2a_{_T}+c_{_T}-b_{_T}-2d\\ &=&b_{_T}+c_{_T}\end{array}$$} The computation for {$\text{GCD}_{_T}\cdot(p^1_b,p^1_b+p^3_b)$} is similar. And finally, {$$\begin{array}{rcl}&&\text{GCD}_{_T}\cdot(p^1_c,p^1_c+p^3_c)\\ &=&(a_{_T}+b_{_T}-c_{_T},d)\cdot(2,2+\frac {c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-2)\\ &=&2a_{_T}+2b_{_T}-2c_{_T}+2d+c_{_T}-a_{_T}+c_{_T}-b_{_T}-2d\\ &=&a_{_T}+b_{_T}\end{array}$$} |