

Billiard Path Segments:Let {$m,n\in\mathbb N$} be the dimensions of a rectangle. Then the length of the path from any corner consists of {$\frac{[m,n]}m+\frac{[m,n]}n-1$} diagonal segments. Proof: From the diagram in Billiards and the LCM, 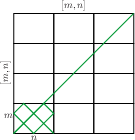 we see that the number of diagonal segments is equal to one more than the number of vertical and horizontal lines crossed. The side of the square is {${[m,n]}$}, so the number of horizontal lines is {$\frac{[m,n]}m-1$}. Similarly, the number of vertical lines is {$\frac{[m,n]}n-1$}, so altogether we have {$\frac{[m,n]}m+\frac{[m,n]}n-2$} lines crossed and {$\frac{[m,n]}m+\frac{[m,n]}n-1$} diagonal segments. |