

Length Computation Subclaim:{$$L_3=I+\left(\frac{c_{_T}-a_{_T}}d+\frac{c_{_T}-b_{_T}}d-1\right)(a_{_T}+b_{_T}-c_{_T}) +\left(\frac{c_{_T}-a_{_T}}d+\frac{c_{_T}-b}d_{_T}-2\right)c_{_T},$$} where {$I$} is the least common multiple of {$c_{_T}-b_{_T}$} and {$c_{_T}-a_{_T}$} and {$d$} is the greatest common divisor. Proof: The formula comes from linking the geodesic on the {$a_{_T}\times b_{_T}\times c_{_T}$} box with the path of a billiard ball bouncing on a {$(a_{_T}-x_{_T})\times(b_{_T}-x_{_T})$} rectangle. The bottom of the {$a_{_T}\times b_{_T}\times c_{_T}$} box 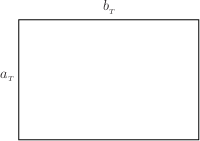 can be centered around a {$(a_{_T}-x_{_T})\times(b_{_T}-x_{_T})$} rectangle. 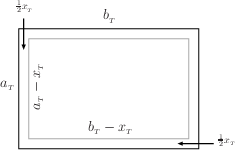 We compare the path of a ball bouncing in the smaller rectangle with a geodesic. 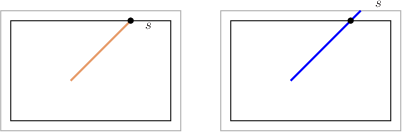 Note where we are after the next diagonals: 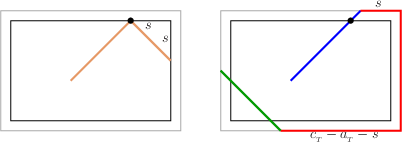 The two points on the inner rectangle are symmetrically opposite, 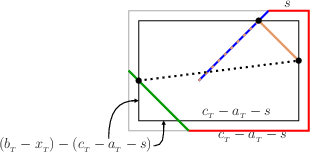 since {$(b_{_T}-x_{_T})-(c_{_T}-a_{_T}-s)=s$}. After another diagonal, the two points will coincide. Consequently, the billiard ball and the geodesic reach their corners in the same number of diagonal moves. The path length of the billiard ball is {$I$}, the least common multiple of the dimensions of the rectangle, {$a_{_T}-x_{_T}$} and {$b_{_T}-x_{_T}$}. For the path length of the geodesic we note that every diagonal is longer by {$x_{_T}$}. Let {$n$} be the number of diagonals. By (a4) of section 1, {$n=\frac {c_{_T}-b_{_T}}d+\frac{c_{_T}-c_{_T}}d-1$} diagonals. This gives us the claim. {$$L_3=I+\left(\frac{c_{_T}-a_{_T}}d+ \frac{c_{_T}-b_{_T}}d-1\right)(a_{_T}+b_{_T}-c_{_T}) +\left(\frac{c_{_T}-a_{_T}}d+\frac{c_{_T}-b}d_{_T} -2\right)c_{_T}.$$} |