

The case of {$\langle y_{_T},y_{_T},-1\rangle $}:The box {$\langle y_{_T},y_{_T},-1\rangle $} has loops iff {$y_{_T}>2$} ({$z_{_T}>1$}). Proof: Let {$j$} be the greatest such that {$\Delta^j(\langle a,b,c\rangle )$} has no negative members. Then {$\Delta^{j+1}(\langle a,b,c\rangle )=\langle u,v,-1\rangle $} and {$\Delta^j(\langle a,b,c\rangle )=\langle u,v,u+v-1\rangle $}. If {$y_{_T}=1$}, then we must have {$j+1=k$} and {$u=v=1$}. Clearly, there are no loops on the {$1\times 1\times1$} box. We can now assume {$y_{_T}\ge 2$}. A GCD Claim: {$(u-1,v-1)=y_{_T}-1$} (using {$(x,y)$} for the greatest common divisor of {$x$} and {$y$}). It is sufficient, in view of Magnified Boxes Have loops, to show that there is a loop on the {$u\times v\times (u+v-1)$} box iff {$y_{_T}>2$}. To do this, we examine the box with each dimension shorter by 1, the {$(u-1)\times(v-1)\times(u-1+v-1)$} box. By the claim, {$u-1=k(y_{_T}-1)$} and {$v-1=l(y_{_T}-1)$} for some {$k,l$} with {$(k,l)=1$}. For simplicity, let {$d=y_{_T}-1$}. So the {$(u-1)\times(v-1)\times(u-1+v-1)$} box is the {$kd\times ld\times (kd+ld)$} box. To understand this box, we'll first look at the {$l\times k\times (k+l)$} box. But in fact, we've already analyzed this box. In the proof of Loopless if {$x_{_T}=0$} and {$z_{_T}=1$} we showed that the eight paths starting on the {$k\times (k+l)$} faces and on the {$l\times (k+l)$} faces have length {$k+l$} and the four paths starting on the {$k\times l$} faces have length {$4k^2+12kl+4l^2-2k-2l$}. These four paths each cut {$k-1+l-1$} edges and so have {$k+l-1$} segments. Now the {$kd\times ld\times (kd+ld)$} box is the {$l\times k\times (k+l)$} box expanded by a factor of {$d$}. Thus it has eight paths of length {$d(k+l)$} and four paths of length {$d(4k^2+12kl+4l^2-2k-2l)$}. Our goal now is the box with each of the dimensions of the previous box increased by 1, the {$(kd+1)\times (kl+1)\times (kd+ld+1)$}, i.e., the {$u\times v\times (u+v-1)$} box. There is a nice relationship between the two boxes. The relationship can be seen by looking at both boxes from above, one superimposed on the other with the base or bottom of the box the face with the shorter two sides. 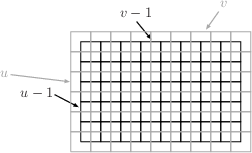 In the proof of Destinations of Paths on Triangular Boxes, case {$a$} and {$b$} odd, it is shown that because the dimensions of the boxes are ``triangular'', that is, no dimension is greater than the sum of the other two, the paths from the corner on the base match. For example, the path in the smaller box, 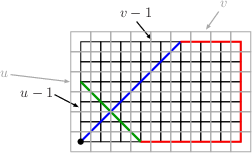 is matched by the one in the larger box. 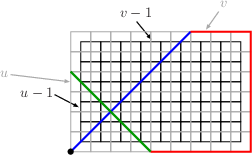 The patterns (the sequence of edges cut) are the same. The difference is that each segment is longer by one in the larger box. Since there are {$k+l-1$} segments for the path on the smaller box, there are {$k+l-1$} segments for the path on the larger box, so the length is increased by {$k+l-1$} to {$d(4k^2+12kl+4l^2-2k-2l)+k+l-1$}. It's a different story for the other eight paths, but a simple one. Paths starting on the {$u\times (u+v-1)$} or the {$v\times (u+v-1)$} faces have length exactly {$2u+2v-1=2(dk+1)+2(dl+1)-1=2dk+2dl+3$}. 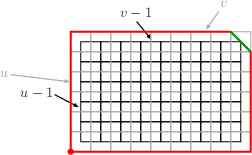 Altogether then, the paths cover {$$4(d(4k^2+12kl+4l^2-2k-2l)+k+l-1)+8(2dk+2dl+3)=12dkl+4dk^2+4dl^2+12dk+12dl+4k+4l-8d+20.$$} If {$y_{_T}=2$}, then {$d=1$} and this reduces to {$$12kl+4k^2+4l^2+16k+16l+12.$$} That is exactly twice the surface area of the box, {$$2((k+1)(l+1)+(k+1)(k+l+1)+(l+1)(k+l+1)),$$} and so there are no loops. On the other hand, if {$y_{_T}>2$}, then {$$\begin{array}{rcl}&&12dkl+4dk^2+4dl^2+12dk+12dl+4k+4l-8d+20\\ &<& 12dkl+4dk^2+4dl^2+16dk+16dl+12\\ &<&12d^2kl+4d^2k^2+4d^2l^2+16dk+16dl+12,\end{array}$$} which is twice the surface area of the box. Thus the box must have loops. |