

|
Case 3: {$a$} and {$b$} odd.  On the bottom, the path can end at the NE corner {$110$}. If {$c$} is even the path will travel on white squares on top and no corner is possible so the destination must be {$110$}. This agrees with the theorem. But if {$c$} is odd, there will be three possible corners: {$110$} on the bottom, {$011$} and {$101$} on the top. Since all three dimensions are odd, let {$a=2k+1$}, {$b=2n+1$}, {$c=2m+1$}. To analyze the situation, we consider a smaller box, the {$2k\times 2n\times 2m$} box.  The paths on the two boxes have the same form, that is, the same sequence of diagonal, vertical and horizontal segments. 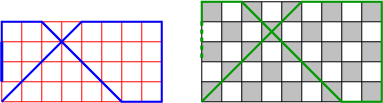 We'll use blue on the smaller box, red on the larger box. And now we'll put one picture on top of the other. 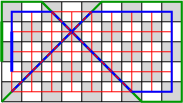 The only tricky part is noting the distance travelled on the sides of the box (the edge of the rectangle). On the smaller box the path travels on the outside a distance of {$2m$} blocks, while on the larger it is {$2m+1$} blocks. 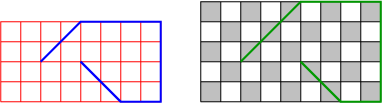 The difference is made up by the fact that the outer path is slowed by exactly two corners. Thus, Case 3 reduces to the smaller box, which falls under Case 1. Note that the differences, {$c-b$} and {$c-a$}, are the same for the two boxes and hence there is no change in the relative evenness. |