

Loopless if {$x_{_T}=0$} and {$z_{_T}=1$}:If {$x_{_T}=0$} and {$z_{_T}=1$} then there are no loops. Proof: Let {$T$} such that {$x_{_T}=0$} and {$z_{_T}=1$} and consider {$\langle a_{_T},b_{_T},c_{_T}\rangle$}. We must have that {$a_{_T}+b_{_T}=c_{_T}$} for {$x_{_T}$} to be zero. If we can show that the box with dimensions {$a_{_T}\times b_{_T}\times (a_{_T}+b_{_T})$} has no loops, then by Proposition 5, we will be done. Applying {$\Delta$} successively to {$\Delta(T)=\langle a_{_T},b_{_T},0\rangle$} is to apply the Euclidean algorithm to {$a_{_T}$} and {$b_{_T}$}, so for {$z_{_T}$} to be 1, we must have that {$a_{_T}$} and {$b_{_T}$} are relatively prime (in the usual sense). We will count the lengths of the paths running from corners and we will see from the sum that the box is covered and consequently there are no loops. First, a path beginning on an {$a_{_T}\times (a_{_T}+b_{_T})$} face ends at the opposite corner with a path length of {$a_{_T}+b_{_T}$}. 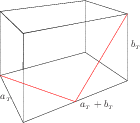 There are eight such paths for a total length of {$8(a_{_T}+b_{_T})$}. For paths beginning on an {$a_{_T}\times b_{_T}$} face, the analysis is similar to that in the proof of Proposition 3. Looking at the box from above, the path is identical to that of a billiard ball bouncing in an {$a\times b$} rectangle. The path of the ball has length the least common multiple of {$a_{_T}$} and {$b_{_T}$}, in this case, {$a_{_T}b_{_T}$}. 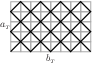 But the path on the box also includes ascending and descending the walls of the box. Each time this takes {$a_{_T}+b_{_T}$} steps. Since you traverse the {$b_{_T}$} direction {$a_{_T}$} times, you hit an {$a_{_T}$} edge {$b_{_T}-1$} times. Since you traverse the {$a_{_T}$} direction {$b_{_T}$} times, you hit an {$b_{_T}$} edge {$a_{_T}-1$} times. Each time you hit an edge, you climb or descend. Thus the number of vertical steps is {$(a_{_T}+b_{_T}) (a_{_T}-1+b_{_T}-1)=a_{_T}^2+2a_{_T}b_{_T}+b_{_T}^2-2a_{_T}-2b_{_T}$}. There are four of these paths so the total of all paths from corners on the box is {$$8(a_{_T}+b_{_T})+4(a_{_T}b_{_T}+a_{_T}^2+2a_{_T}b_{_T}+b_{_T}^2-2a_{_T}-2b_{_T})=4a_{_T}^2+12a_{_T}b_{_T}+4b_{_T}^2.$$} On the other hand, the surface area of the box is {$2(a_{_T}b_{_T}+a_{_T}(a_{_T}+b_{_T})+b_{_T}(a_{_T}+b_{_T}))$}}. We multiply this by 2 because covering the box means running across each square twice, once in each direction. This gives us {$$4(a_{_T}b_{_T}+a_{_T}(a_{_T}+b_{_T})+b_{_T}(a_{_T}+b_{_T}))=4(a_{_T}b_{_T}+a_{_T}^2+a_{_T}b_{_T}+b_{_T}a_{_T}+b_{_T}^2)= 4a_{_T}^2+12a_{_T}b_{_T}+4b_{_T}^2,$$} the same number. So the paths from the corners completely cover the box---there are no loops. |