

Computing the destination with a Rubik's cube.We can identify the corners of the cube with the labels set up in Triangularity, except this time we have positioned the origin behind the cube. 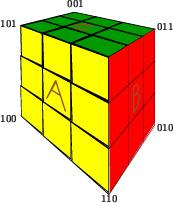 Label the faces A, B, C as above. Now suppose we are given an {$a\times b\times c\times$} box. If the numbers aren't triangular, subtract the two lowest from the largest. Continue this until the trio is triangular. All the while, note each time which of the three dimensions is being reduced. For an example, suppose we have 65, 35, and 123. This reduces like this:
Next, we use Square Bottom, Sum of Two, Just Right, or Destinations of Paths on Triangular Boxes to determine the destination for the reduced trio. In the case of (5, 7, 11), it is {$101$}. We mark this on the cube. 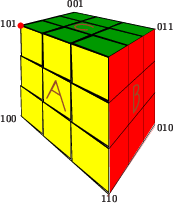 Now we turn the faces of the cube 180 degrees according to the sequence of letters, but in reverse order, turning the C face, then the B face, then the A face, then the C face again. 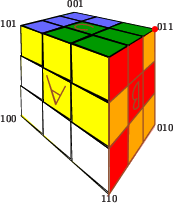 The marked corner has moved. It's at the {$011$} location. That's the destination for the box with dimensions (65,35,123). |