

TriangularityDefinition:The {$a\times b\times c$} box is triangular if {$a\le b+c$}, {$b\le a+c$}, and {$c\le a+b$}. On the box triangle, triangular boxes are the points in the center. 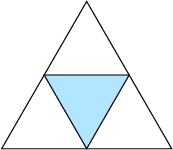 Triangular boxes are special, but boxes in general can be reduced to triangular boxes. Definition:The {$\Delta$} function acts on unordered triples of numbers by subtracting the two smaller numbers from the largest number. For the {$a\times b\times c$} box {$T$}, with {$a\le b\le c$}, {$\Delta (T)$} is the {$a\times b\times (c-a-b)$} box. To show how destinations on boxes in general reduce to destinations on triangular boxes, we need some notation. First, we locate the {$a\times b\times c$} box in what we will call "standard position." We place the box in the first octant of {$\mathbb R^3$} with one corner at the origin and one at {$(a,b,c)$}, with an edge of length {$a$} along the {$x$} axis, an edge of length {$b$} along the {$y$} axis, an edge of length {$c$} along the {$z$} axis. 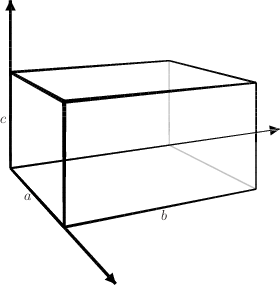 And the path will start at the origin and move along the {$a\times b$} face. 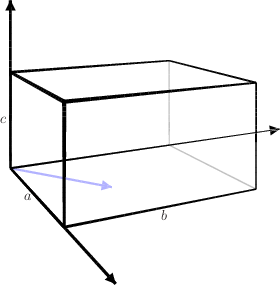 Now we label the corners as follows. 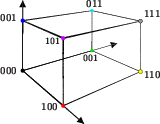 Let the destination of the path on the {$a\times b\times c$} box be {$\ \ $} xyz. Then
We can see the effect of this proposition in the box triangle. If we systematically take points in the triangle, examine the corresponding box, note at which corner the path ends, and then color the point appropriately, we get this picture:  This picture is closely connected to the Rauzy gasket. Back to Geometry. |