

{$\Delta$} and Destinations:Let the destination of the path on the {$a\times b\times c$} box be {$\ $} xyz. Then
Proof: This proposition is the chief reason for the labels on the corners, 000, 001, ... 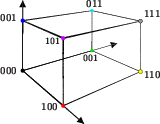 If the first character is 0, then the corner is in the {$yz$}-plane (the {$x$} coordinate is {$0$}). If the first character is 1, then the corner is in the plane {$x=a$}. Similarly, the second character registers whether the corner is in the plane {$y=0$} or the plane {$y=b$}. The effect of adding to one dimension the sum of the other two can be described in terms of the characters of the labels. Suppose, for example, {$a$} and {$c$} are added to {$b$}.  The additional length rotates a path traversing the {$b$} direction exactly 180 degrees.  If the destination on the smaller box is on the left, that is, if y=0, then the path will travel the {$b$} length of the box an even number of times. Then the path will be rotated an even number of times so there will be no effect on the destination, which coincides with the statement in the proposition, since xyz{$=$}(x{$\oplus$}y)y(z{$\oplus$}y) when y=0. On the other hand, if the destination on the smaller box is on the right, that is, y=1, then this has the effect of changing the ending corner's other two coordinates. Again, this agrees with the statement. |