

Generalized Continued FractionsContinued fractionsConsider two maps, {$L$} and {$R$} on {$\mathbb {N}^2$}: {$$L(m,n)=(m+n,n)$$} {$$R(m,n)=(m,m+n)$$} and a valuation, {$$V(m,n)=\frac mn$$} Then any finite continued fraction, any rational number, is equal to the value of a finite composition of {$L$} and {$R$} applied to {$(0,1)$}. For example, {$$2+\frac 1{3+\frac 1{1+\frac 1{3+\frac 11}}}$$} is equal to {$$V[L^2R^3L^1R^3L^1(0,1)]=\frac {43}{19}.$$} An infinite continued fraction, {$$2+\frac 1{3+\frac 1{1+\frac 1{3+\frac 1{\ddots}}}}$$} is equal to the limit of the sequence, {$$V[L^2(1,1)],\ V[L^2R^3(1,1)],\ V[L^2R^3L^1(1,1)],\ V[L^2R^3L^1R^3(0,1)],\ \ V[L^2R^3L^1R^3L^1(0,1)],\ \ldots$$} Continued TractionsFor our generalized continued fraction, consider four maps, {$L$}, {$R$}, {$M$} and {$C$} on {$\mathbb {N}^3$}: {$$L(a,b,c)=(a+b+c,b,c)$$} {$$R(a,b,c)=(a,b,a+b+c)$$} {$$M(a,b,c)=(a,a+b+c,c)$$} {$$C(a,b,c)=(b+c,a+c,a+b)$$} and a valuation, {$$V(a,b,c)=\left(\frac a{a+b+c},\frac b{a+b+c}\right)$$} These functions are inspired by the Euclidean algorithm for boxes and the box triangle. {$L$} maps the entire triangle to the lower-right fourth (sorry, left and right get switched here).  {$M$} maps the triangle to the upper fourth,  and so on. A finite generalized continued fraction is the valuation of a composition of {$L$}, {$R$}, {$M$} and {$C$} applied to {$(1,1,1)$}. We can't quite achieve all points in the box triangle from this. We miss the rims. Here, for example, is the point {$\left(\frac 37,\frac 15,\frac {13}{35}\right)$}, or, {$\left(15,7, 13\right)$}. 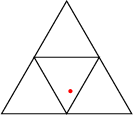 This is in the center, so the first function we will use is {$C$}. If I apply the inverse of {$C$}, {$$C^{-1}(a,b,c)=(b+c-a,a+c-b,a+b-c),$$} we get {$(5,21,9)$} 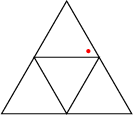 This is in the upper fourth, so we use {$M$}. Applying the inverse of {$M$}, {$$M^{-1}(a,b,c)=(a,b-a-c,c),$$}, we get {$(5,7,9)$} 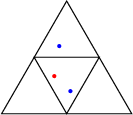 That's {$C$} again. We keep going, 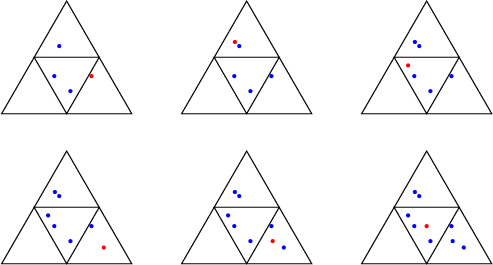 with the functions: {$L$}, $M$}, $C$}, $L$}, $L$}. This checks: {$$V[CMCLMCLL(1,1,1)]=V[(120,56,104)]=V[(15,7,13)]= \left(\frac 37,\frac 15,\frac {13}{35}\right).$$} Finally, an infinite generalized continued fraction is, as in the ordinary case, the limit of finite compositions. |