

Easy First StepsA Euclidean Algorithm for Boxes The ordinary Euclidean algorithm could be described as the repeated action of subtracting the smaller from the larger of two numbers. We know that a pair of numbers are relatively prime if and only if this action eventually results in the numbers 0 and 1, for example, from this
we see that 39 and 50 are relatively prime. We do something very much like this at several places on this website. The delta function, {$\Delta$}, subtracts the two smaller numbers from the largest of a trio of numbers. This will be our Euclidean Algorithm for Boxes. Classifying Boxes Definition: Let {$\mathcal B$} be the space of all unordered triples of integers (not necessarily distinct). Let {$\mathcal {B}^+$} be the set of unordered triples of positive integers. Think of {$\mathcal {B}^+$} as the collection of shapes of boxes. We will use "box" for a member of {$\mathcal{B}^+$} as well as for the geometric object. We will use angle brackets, {$\langle a,b,c\rangle$}, for members of {$\mathcal {B}$}. What {$\Delta$} Does: For {$T\in \mathcal {B}^+$}, {$k\in\mathbb N$},
Definition: We say {$T\in \mathcal{B}^+$} is "terminating" if for some {$k\in\mathbb{N}$}, {$\Delta^k(T)=\Delta^{k+1}(T)$}. This happens only when the two smaller numbers add to zero. All Terminate: Every {$T\in \mathcal{B}^+$} is terminating. Definition: For {$T\in \mathcal{B}^+$}, let {$x_{_T}$}, {$y_{_T}$} be such that for some {$k$}, {$\Delta^k(T)=\langle x_{_T},y_{_T}, -x_{_T}\rangle$}. Let {$z_{_T}=y_{_T}-x_{_T}$}. By What {$\Delta$} Does, we know {$z_{_T}>0$}. Definition: ''For {$T\in \mathcal{B}^+$}, let {$k$} be greatest such that {$\Delta^k(T)$} has only positive members and let {$\Delta^k(T)=\{a_{_T}, b_{_T}, c_{_T}\}.$}. We can use {$a_{_T}, b_{_T}, c_{_T}, x_{_T}, y_{_T}, z_{_T}$} to classify four distinct types of boxes. These types will be useful soon in proofs. Definition: A box {$T\in\mathcal {B}^+$} is an "axle" if {$z_{_T}=0$}. Equivalently, an axle is a box where {$x_{_T}=y_{_T}$}. Equivalently, an axle is a box where {$a_{_T}=b_{_T}=c_{_T}=x_{_T}$}. In the box triangle, axles are the centers of the triangles. 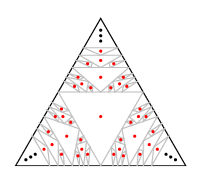 Definition: A box {$T\in\mathcal {B}^+$} is a "spoke" if it is not an axle, but the two largest of {$a_{_T},b_{_T},c_{_T}$} are equal. In the box triangle, spokes connect the centers of the triangles with their vertices.  Definition: A box {$T\in\mathcal {B}^+$} is a "rim" if {$x_{_T}=0$}. A triangular rim is a box of the form, {$a\times b\times (a+b)$}. In the box triangle, rims form the borders of the triangles.  If we think of a rectangle as a box of height 0, then rectangles are rims. Definition: Boxes which are not axles, spokes or rims are "generic".  |