

Bi-infinite Geodesics:Almost every box has a geodesic that is infinite in both directions. Proof: First, we claim that Almost Claim Almost every box's dimensions are linearly independent over the rationals. Now let {$a\times b\times c$} be a normal box with linearly independent dimensions. The work of {$T$} is loopless iff {$\Delta T$} is loopless shows that we can assume the box is strictly triangular. We'll say {$a<b<c<a+b$}. Using the overhead view, we examine geodesics that cross the bottom of the box moving southwest-northeast. There are, first of all, the paths that begin and end at corners on the top (Just Right), this one, 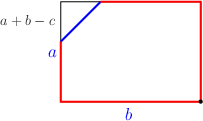 and this one.  There are also two paths infinite in one direction starting from corners on the bottom (Irrationals and Infinite Paths). This is how they begin-- 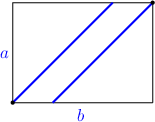 Together, these account for all geodesics crossing the bottom in the NE-SW direction which hit corners. There are also loops. It's not hard to see that any geodesic hitting the yellow edges are loops,  for example, 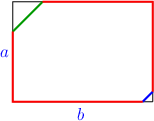 It follows that any NE-SW geodesic hitting the brown edges are either loops or paths infinite in both directions. 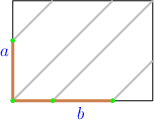 But such a geodesic 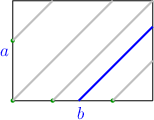 can't be a loop, for if it were, we could slide it slowly toward one of the infinite geodesics. 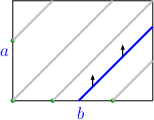 Because it wouldn't hit a corner, it would continue to be a loop. But then the infinite geodesic would also have to be a loop, a contradiction. |