• View
• Print
• Backlinks

Third of Center:

For any {$0<r<\frac12$}, all the triples on the line between {$\left(r,\frac12-r,\frac12\right)$} and {$\left(\frac13,\frac13,\frac13\right)$} (the dashed line in the picture below) are colored the same. In particular, either for all the boxes the paths are finite or for all they are infinite.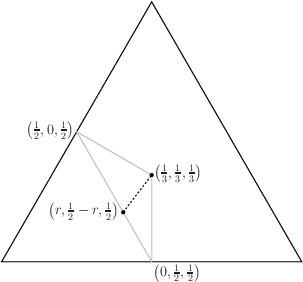

Proof:

Before we start, it will be useful to call any expression of the form:

[some linear function of {$r$}]{$\cdot t+2$}

as "equivalent to {$2$} mod {$t$}" and any expression of the form

[some linear function of {$r$}]{$\cdot t$}

as "equivalent to {$0$} mod {$t$}". The point of this is that if two expressions are equivalent mod {$t$}, then whether their difference is positive, negative, or zero is independent of the value of {$t$} (which will be positive).

Now the points on the dashed line above are parametrized by {$t$} as follows: {$$\left(r,\frac12-r,\frac12\right)t+\left(\frac13,\frac13,\frac13\right)(1-t)$$} for {$0<t\le 1$}. To simplify matters we combine these {$$\left(\left(r-\frac13\right)t+\frac13, \left(\frac16-r\right)t+\frac13,\frac16t+\frac13\right)$$} and multiply by 6 (which doesn't affect the path pattern), {$$(6r-2)t+2, (1-6r)t+2,t+2)$$} So all dimensions of the box are equivalent to {$2$} mod {$t$}.

We will show that the pattern of the path, as described by the particular edges crossed and the particular walls traversed, is independent of {$t$}. We use the overhead view, first as the path as it crosses the bottom,

then as it continues on, climbing up the sides of the box.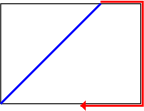

The pattern at the start depends on which of the dimensions of the bottom is larger, {$(6r-2)t+2$} or {$(1-6r)t+2$}. That is independent of {$t$}; the difference between the two side-lengths is equivalent to {$0$} mod {$t$} and is positive or negative depending on the relative sizes of {$6r-2$} and {$1-6r$}.

The next part of the pattern is set since we know that in climbing the sides, the path passes exactly two corners (the Two Corners Claim).

We will show for each step:

1. Which edge is reached is independent of {$t$}.
2. Whenever an edge on the bottom or top is reached, it is at a point dividing the edge into two pieces where one of the pieces is and the other is equivalent to {$0$} mod {$t$}.
3. Whenever you are about to climb a wall or descend a wall, you move in the direction of the segment equivalent to {$0$} mod {$t$}.
4. Whenever you are about to cross the bottom or the top of the box, you move in the direction of the segment equivalent to {$2$} mod {$t$}.

Statements 1., 2. and 3. are clearly true at the start. The segments are either {$(6r-2)t+2$} and {$(3-12r)t$} if {$(1-6r)t+2>(6r-2)t+2$},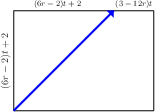

or {$(1-6r)t+2$} and {$(12r-3)t$} if {$(6r-2)t+2>(1-6r)t+2$}.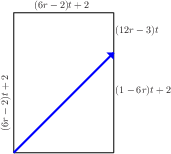

Both {$(3-12r)t$} and {$(12r-3)t$} are equivalent to {$0$} mod {$t$}.

Since the height and the sides of the box are all equivalent to {$2$} mod {$t$}, 4. is true when we reach the top.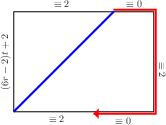

What matters next is which side is hit by the subsequent diagonal path across the top. This is determined by comparing the sizes of two lengths, both equivalent to {$2$} mod {$t$} That determination, as before, is independent of {$t$}, depending only on the coefficients of {$t$}, verifying 1. And whichever side is reached by the diagonal,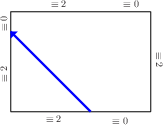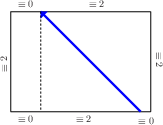

2. and 3. continue to be true. As before, 4. will be true as well, since the path always rounds two corners when climbing or descending (again, the Two Corners Claim).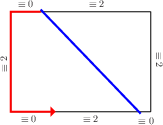

This shows that the pattern of the path is the same for all values of {$t$} between {$0$} and {$1$}. Further, whether or not a corner is reached and the path ends is likewise independent of {$t$}. This completes the proof.