

The Path Vector Claim:Let {$\vec P^1$} and {$\vec P^3$} be paths on {$T=\langle r,s,t\rangle$} corresponding to {$L_1$} and {$L_3$} of {$\text{LCM}_{_T}$}. If
then the proposition, {$\text{GCD}\cdot\text{LCM}=\text{PROD}$}, holds for the three pre-images. Proof: We won't do all three here, they are similar. We will address the second pre-image. Let {$T'=\langle r,s+r+t,t\rangle$}. We have {$$\text{GCD}_{_T}=\text{GCD}_{_{T'}}$$} but {$$\text{LCM}_{_T}<>\text{LCM}_{_{T'}}.$$} {$\text{LCM}_{_T}=(L^1,L^1+L^3)$}, (since {$L^1=L^2$}, see At Most Three Paths) and each {$L^i$} equals {$P^i\cdot T$}, so {$$\text{LCM}_{_T}=\frac12 (P^1\cdot T, P^1\cdot T+ P^3\cdot T),$$} where {$\vec P^1=(p^1_a,p^1_b,p^1_c)$} and {$ \vec P^3=(p^3_a,p^3_b,p^3_c)$} are the respective path vectors for {$\vec P^1$} and {$\vec P^3$} and {$ T$} is the vector {$(r,s,t)$}. As you can see from this figure, 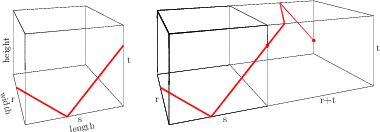 increasing the length by {$r+t$} means that the path vector for {$\vec {P^1}'$} is {$(p^1_a+p^1_b,p^1_b,p^1_c+p^1_b)$} because every time the length is traversed ({$p^1_b$} times), the width and the height get an additional traverse, but there are no additional traverses for length. We can describe this with two linear transformations: {$$J(u,v,w)=(u+v,v,w+v)$$} {$$H(u,v,w)=(u,u+v+w,w).$$} {$H(T)$} is {$T'$}, the second pre-image and {$J(\vec P^1)$} is the path vector of the path on {$T'$} corresponding to {$\vec P^1$}. Then {$$\text{LCM}{_{_{T'}}}=\frac12 (J(\vec P^1)\cdot H(T), J(\vec P^1)\cdot H(T)+ J(\vec P^3)\cdot H(T)).$$} Computing the difference between {$\text{GCD}_{_T}\cdot \text{LCM}{_{_{T'}}}$} and {$\text{GCD}_{_T}\cdot\text{LCM}_{_T}$}, {$$J(\vec P^1)\cdot H(T)-\vec P^1\cdot T=(p^1_a+p^1_b)r+p^1_b(s+r+t)+(p^1_c+p^1_b)t) =2p^1_b(r+t),$$} so {$$\text{LCM}_{_T'}-\text{LCM}_{_T}=(2p^1_b(r+t),2p^1_b(r+t)+2p^3_b(r+t))=(r+t)(p^1_b,p^1_b+p^3_b)$$} and {$$\text{GCD}{_{_{T'}}}\cdot\text{LCM}{_{_{T'}}}-\text{GCD}_{_T}\cdot\text{LCM}_{_T}=(r+t)\text{GCD}_{_T} \cdot(p^1_b,p^1_b+p^3_b).$$} Then by statement 2., this is {$(r+t)^2$}. But a simple computation (see Product) shows that {$\text{PROD}{_{_{T'}}}-\text{PROD}_{_T}$} is also {$(r+t)^2$} so the proposition, {$\text{GCD}{_{_{T'}}}\cdot\text{LCM}{_{_{T'}}}=\text{PROD}{_{_{T'}}}$}, holds. |