

Spokes and Generic Boxes and the GCD:For all spokes and generic boxes, {$\langle a,b,c\rangle$}, {$\frac{N(\langle a,b,c\rangle)}2+2=x_{_T}+y_{_T}-1$}. Proof: Spokes and generic boxes are characterized by {$x_{_T},z_{_T}\neq0$} and hence {$x_{_T}\neq y_{_T}$}. Let {$k$} be such that {$\Delta^k(\langle a,b,c\rangle )=\langle x_{_T},y_{_T},-x_{_T}\rangle $}. By proposition 17, {$N(\langle a,b,c\rangle )=N(\langle x_{_T},y_{_T},-x_{_T}\rangle )=N(\langle x_{_T},y_{_T},y_{_T}\rangle )$}. We will show that the {$x_{_T}\times y_{_T}\times y_{_T}$} box has exactly {$2(x_{_T}+y_{_T}-1)$} loops. From that we conclude that the {$a\times b\times c$} box also has {$2(x_{_T}+y_{_T}-1)$} and so {$G(\langle a,b,c\rangle )=\frac12\cdot2(x_{_T}+y_{_T}-3)+1=x_{_T}+y_{_T}-2$}. At each of the integral points along two sides of the bottom of the {$x_{_T}\times y_{_T}\times y_{_T}$} box imagine a geodesic moving in a clockwise direction. Note {$x_{_T}\le y_{_T}$} from Proposition 4. 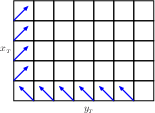 One of these is not a loop because it immediately leads to the corner at the upper left. 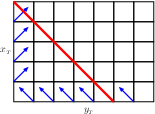 Each of the others is a loop, 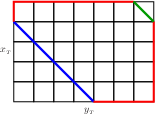 and they are all different. 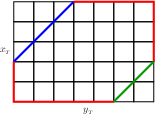 This follows easily from the fact that the height of the box is {$y_{_T}$}. This gives us {$(x_{_T}-1)+(y_{_T}-1)-1=x_{_T}+y_{_T}-3$} loops. But for each loop here 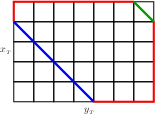 there is symmetric loop with the top and bottom parts exchanged. 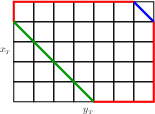 |