

|
The surprising fact is that on this highly irregular box, if you start at one corner, moving on the surface at an angle of 45 degrees from the edges, the path doesn't go on forever. It returns to its starting point. 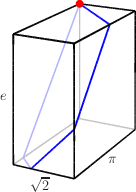 This is completely different from what happens to a billiard ball bouncing in a rectangle. Infinite Billiard Paths states that if the dimensions of a rectangle do not have a rational ratio, then the ball bounces forever. |