

Respecting Loops on Boxes with Negative Height:For all {$a,b\in\mathbb N^+$}, {$c\in\mathbb Z$}, {$c<0$}, {$a+b+c>0$}, {$N(\langle a,b,c\rangle )=N(\langle a,b,a+b+c\rangle )$}. Proof: Suppose you have a loop on the {$a\times b\times a+b+c$} box. It may begin like this: 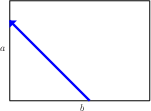 then it winds around a distance of {$a+b+c$}, 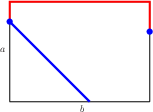 which is {$-c\ $} short of {$a+b$}. 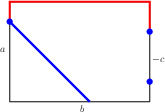 But on the {$a\times b\times c$} box, a path starting at the same place would not move clockwise around the rectangle but counter-clockwise, a distance of {$-c$}. That puts it directly opposite where the path on the {$a\times b\times a+b+c$} goes. 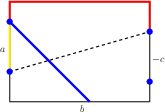 After two more moves, the points will be the same. Every two moves, that is, every time the paths climb or descend the sides, the orientations change 180 degrees. Since the sides must be climbed and descended an even number of times (this is a loop), the paths must end up together. Thus, a loop on the {$a\times b\times a+b+c$} box generates a loop on the {$a\times b\times c$} box. In a similar way, a loop on the {$a\times b\times c$} box generates a loop on the {$a\times b\times a+b+c$} box. |