

Axles and the GCD:For all axles, {$\langle a,b,c\rangle$}, {$\frac{N(\langle a,b,c\rangle)}2+2=x_{_T}+y_{_T}$}. Proof: Let {$k$} be least such that {$\Delta^k(\langle a,b,c\rangle )=\langle x_{_T},x_{_T},-x_{_T}\rangle $}. Then {$\Delta^{k-1}(\langle a,b,c\rangle )=\langle x_{_T},x_{_T},x_{_T}\rangle $} (that is, {$a_{_T}=b_{_T}=c_{_T}=x_{_T}=y_{_T}$}). By {$\Delta$} Respects Loops, {$N(\langle a,b,c\rangle=\langle x_{_T},x_{_T},x_{_T}\rangle $}. A typical loop on the {$x_{_T}\times x_{_T}\times x_{_T}$} box looks like this: 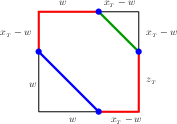 This is part of a family of eight loops, all with the same proportions. Four have their diagonals going SW-NE, four have their diagonals going SE-NW. If {$x_{_T}$} is odd, the number of such families is {$\frac{x_{_T}-1}2$}, so the total number of loops is {$\frac{x_{_T}-1}2\cdot 8=4x_{_T}-4$}. Thus, {$$\frac{N(\langle a,b,c\rangle)}2+2=\frac12(4x_{_T}-4)+2=2x_{_T},$$} which is {$x_{_T}+y_{_T}$} when {$x_{_T}=y_{_T}$}. On the other hand, if {$x_{_T}$} is even, the loop in the middle, 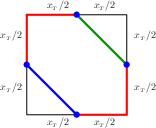 is part of a family of four loops so the total number of loops is {$$1\cdot4+\frac{x_{_T}-2}2\cdot 8=4x_{_T}-4,$$} so that again {$\frac{N(\langle a,b,c\rangle)}2+2=x_{_T}+y_{_T}$} (since {$x_{_T}=y_{_T}$}). |