• View
• Print
• Backlinks

Also True for {$T'$} Claim:

Let {$P^1$} and {$P^3$} be paths on {$T'=\langle a_{_T},b_{_T},c_{_T}\rangle$} corresponding to {$L_1$} and {$L_3$}. Then

• {$\text{GCD}_{_{T'}}\cdot(p^1_a,p^1_a+p^3_a)=(b_{_T}+c_{_T})$}
• {$\text{GCD}_{_{T'}}\cdot(p^1_b,p^1_b+p^3_b)=(a_{_T}+c_{_T}).$}
• {$\text{GCD}_{_{T'}}\cdot(p^1_c,p^1_c+p^3_c)=(a_{_T}+b_{_T}).$}

Proof:

For the path of length {$L_1=L_2=a_{_T}+b_{_T}$},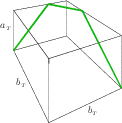

the path vector is {$(2,1,1)$}. For the path of length {$L_3=b_{_T}$}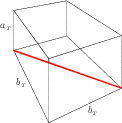

the path vector is {$(0,1,1)$}. So {$$\begin{array}{rcl}\text{GCD}_{_T}\cdot(p^1_a,p^2_a+p^3_a) &=&(b_{_T}-a_{_T},a_{_T})\cdot(2,2)\\ &=&2b_{_T}\end{array}$$} and {$$\begin{array}{rcl}\text{GCD}_{_T}\cdot(p^1_b,p^2_b+p^3_b) &=&(b_{_T}-a_{_T},a_{_T})\cdot(1,2)\\ &=&a_{_T}+b_{_T}\end{array}$$} and {$$\begin{array}{rcl}\text{GCD}_{_T}\cdot(p^1_c,p^2_c+p^3_c) &=&(b_{_T}-a_{_T},a_{_T})\cdot(1,2)\\ &=&a_{_T}+b_{_T},\end{array}$$} and the statements are established for {$T'=\langle a_{_T},b_{_T},c_{_T}\rangle$}.